B09 [宿題]

B09_1 (スクリプト)

ねらい: 関数の作成に慣れる．

文字列の引数 inputstr, trgt の2つを引数として，inputstr の中から trgt の値を検索し，見つかったら「＜trgtの値＞を見つけました！」と表示する関数 findipt() を作成しなさい．ただし，文字列中に複数の＜trgtの値＞が存在していても，「見つけました」と表示するのは一度で良い．また，文字列の引数 inputstr, trgt の2つを引数として，inputstr の中に含まれる trgt の値の文字列の数を計算し，「＜trgtの値＞の数は＜trgtの値の個数＞個です！」と表示する関数 countipt() を作成しなさい．

次に，起動すると「文字列を入力して下さい．」と表示して入力を促し，文字列が入力されたら続いて「探す文字列を指定して下さい．」と表示し，入力された文字列をそれぞれ引数 inputstr, trgt に渡して findipt(), countipt() を呼び出すスクリプトを作成しなさい．

実行結果のスクリーンショット B09_1.png と B09_1.py を提出しなさい．

B09_2 (スクリプト&インタラクティブシェル)

ねらい: モジュールの作成に慣れる．map 関数で関数を対象に一様に適用する方法を学ぶ．

1から5の，5つの整数を要素とするリストと6から10の，5つの整数を要素とするリスト（2つのリスト）を要素とする listex（[ [1,2,3,4,5],[6,7,8,9,10]]）と，課題A09_1で作成した関数 heikin(x) の2つのオブジェクトを含んだファイルを作成し，B09_2.py としなさい．

インタラクティブシェルで，上記で作成したモジュール B09_2 をインポートし，listex の2つの要素の平均値をそれぞれ求めて，リストとして画面に表示しなさい．

実行結果のインタラクティブシェルのスクリーンショット B09_2.png と B09_2.py を提出しなさい．

B09_3 (スクリプト)

ねらい: 再帰的関数の作成を学ぶ．

課題B06_3で実習したユークリッドの互除法で最大公約数をもとめる方法を関数を以下のように作成しなさい．

自然数の最大公約数は以下の手順で求められる．これをユークリッドの互除法という．

  1. 小さい整数を変数 y，大きい整数を変数 x として x を y で割り，その余りで yを割る．
  2. 次に，ステップ1の割る数 y をステップ1の余りで割る...

これを繰り返して，計算結果が割り切れるまで続ける．最後の割る数 y が最大公約数である． 関数名と引数は gcd(x, y) とし，関数の中で gcd(x, y) を呼び出すことで繰り返しの計算を実現しなさい．

次に，input を2回使ってキーボードから大きい整数と小さい整数を入力し，これらを関数 gcd(x, y) に渡して最大公約数を求めて表示するスクリプトを作成して B09_3.py としなさい． なお，ユーザーが1番目の input で大きい数の方を入力しても2番目の input で大きい数の方を入力しても正しい結果が出るようにせよ． スクリプトには関数 gcd(x, y) も一緒に記述すること．

実行結果のスクリーンショット B09_3.png と B09_3.py を提出しなさい．

ユークリッドの互除法の計算の例 

>>> 3355 % 2379
976
>>> 2379 % 976
427
>>> 976 % 427
122
>>> 427 % 122
61
>>> 122 % 61
0

B09_4 (スクリプト&インタラクティブシェル，オプション)

ねらい: 関数とモジュールの作成を学ぶ．インタラクティブシェルからモジュールをインポートして実行する方法を学ぶ．

学籍番号の下4桁（例:1234）を引数にとり，各位の数字を要素に持つ4要素のリスト（例：[1, 2, 3, 4]）を返す関数 henkan(x) を作成し，課題A09_1で作成した関数heikin(x)，課題A09_2で作成した関数 bunsan(x) とあわせて B09_4.py ファイルに記述して，B09_4モジュールを作成しなさい．

さらに，以下の手順をインタラクティブシェルで実行して，実行結果のスクリーンショットを撮りなさい．

  1. インタラクティブシェルから，B09_4モジュールをB94としてインポートしなさい．
  2. 自分の学籍番号の下4桁（例:1870）を引数として henkan(x) を実行し，戻り値を bangou に代入しなさい．このとき bangou を表示すると，学籍番号の下4桁（例:1870）の各位の数字のリストが表示される（例：[1, 2, 3, 4]）．
  3. bangou を引数として heikin(x) を実行して平均値を表示しなさい．
  4. bangou を引数として bunsan(x) を実行して分散を表示しなさい．

インタラクティブシェルの実行結果のスクリーンショット B09_4.png と B09_4.py を提出しなさい．

※ヒント：文字列のリスト strlist = ['1' , '2' , '3' , '4'] を整数のリスト[1, 2, 3, 4]に変更するには，map 関数を用いて関数 int を文字列リスト strlist に適用すればよい．

B09_5 (スクリプト，オプション)

ねらい:再帰的な呼び出しという概念を理解する．

以下は10から1ずつ減算した値を順に1まで表示するつもりで作成したスクリプトであるが，バグがあって10個の0が連続して表示される．バグを修正したスクリプトを B09_5.py として実行し，画面に10から1ずつ減算した値を順に1まで表示しなさい．

実行結果のスクリーンショット B09_5.png と B09_5.py を提出しなさい．

def decreaseref(y):
    y -= 1
    if y > 0:
        y = decreaseref(y)
    print(y)
    return y

decreaseref(10)

B09_6 (スクリプト，オプション)

ねらい: 再帰的関数によるタートルグラフィックを学ぶ．

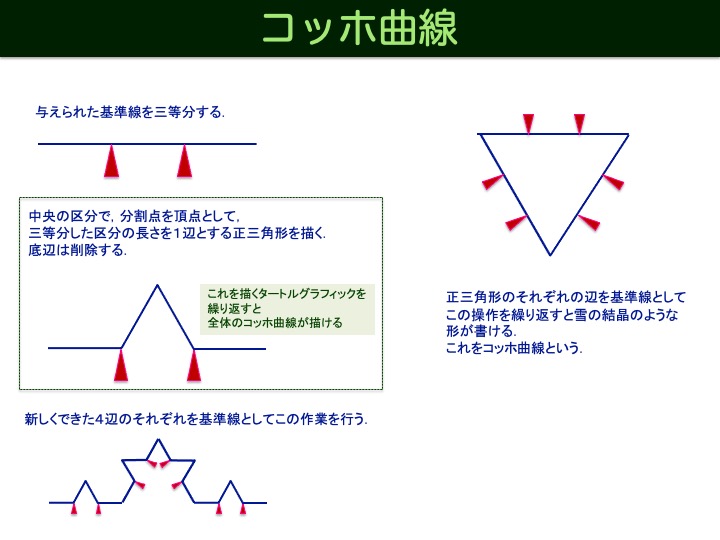
タートルグラフィックを用いて，コッホ曲線を用いた雪の結晶のような形を描画しなさい（図を参照）． 但し，再帰呼び出しの回数 generation，分割される線分の長さ length を引数にとる関数 koch(generation, length) を作成し，これを関数 koch() の内部から呼び出す再帰的呼び出しを利用しなさい．このスクリプトを B09_6.py として提出しなさい．また，タートルグラフィックの画面を B09_6.png として提出しなさい．

コッホ曲線

＊コッホ曲線とは，線分を3等分し，分割した2点を頂点とする正三角形の作図を無限に繰り返すことで作成される図形である． 作成方法は，以下の図を参照しなさい．

コッホ曲線の作成